Ch1 行列式
一些定义
n阶行列式
n阶行列式的值是一个数
余子式
代数余子式
n阶行列式的值的定义(公式)
行列式的性质
行列式与其转置的行列式相等：$D^T=D$
证明：数学归纳法
数乘：第二类初等变换
行列式的某一行（列）都乘以k，等于用k乘以行列式：
推论：如果行列式某一行（列）都是0，则行列式为0
交换行列式的两行，行列式反号
推论：若行列式两行（列）元素对应相等（成比例），行列式值为0
推论：行列式任一行的所有元素与另一行对应元素的代数余子式乘积之和等于零
证明：放入新行列式$D_1$中，$D_1$有两行元素相同，故$D_1=0$
所以有：
拆项：
第三类初等变换：
行列式的计算
利用行列式的性质，使得要计算的行列式中有尽可能多的0，从而降阶和简化计算
三角行列式,$D=a_{11}a_{22}…a_{nn}$，只与主对角有关
爪型行列式（P15）
Vandermonde行列式P16
三对角行列式P18
Cramer法则
证明用到了定理，
齐次方程组的非零解
Ch2 矩阵
(行列式的)一些性质
矩阵无乘法交换律
矩阵有：结合律、分配律、数乘
矩阵的行列式，有性质： $$ det(kA)=k^ndet(A) $$
$A^{T}$的性质
矩阵转置的行列式不变（数学归纳法） $$ \Rightarrow |A^T|=|A| $$
$$ r(A^TA)=r(A)=r(A^T) $$
可逆矩阵
可逆矩阵一定是方阵
可逆矩阵的逆矩阵是唯一的
证明 $A可逆 \Leftrightarrow det(A)=0$ ：
通过$A^*$求$A^{-1}$
伴随矩阵：$A^$是$A$每个元素换成其对应的代数余子式，然后取转置得到的矩阵,且有： $$ A^{-1} = \frac{A^}{det(A)} $$
逆矩阵的性质
最重要的：$AB = BA$
分块矩阵
乘法、逆、转置
对角分块矩阵的逆：
矩阵的初等变换
行阶梯形与行标准形
标准形
初等矩阵：对单位矩阵$I$实施一次初等变换得到的矩阵，成为初等矩阵
行初等与列初等，各自分为三种
对矩阵$A$实施一次行初等变换，相当于用相应的初等矩阵左乘；列初等变换相当于用相应的初等矩阵右乘
矩阵等价：
自反、对称、传递
初等变换求逆法：
矩阵的秩
性质：
$$
满秩 \Leftrightarrow 可逆 \Leftrightarrow det(A) \ne 0
$$
初等变换不改变矩阵的秩
有关秩的定理：
矩阵乘积的秩不超过每个因子的秩： $$ r(AB) \le min { r(A), r(B)} $$ Sylvester公式：
还有：
Ch3 向量
除非特别说明，所有向量都指列向量
运算
线性运算：加法与数乘
向量组的线性相关性
线性组合
线性无关/相关：
即，仅当k1…kn都为0时向量的线性组合才为0，时，线性无关
若线性无关，则说明“不共线”(几何意义)
向量组$\left { \alpha_1, \alpha_2, \alpha_3…, \alpha_m \right } $线性无关 $\Leftrightarrow$ 其中至少有一个向量是其余向量的线性组合
性质：(好像没用)
向量组的极大线性无关组
等价的向量组：
由此引出极大线性无关组
给定一个向量组，它的任何两个极大线性无关组都是等价的，从而所含向量一样多，因此：
向量组的秩与矩阵的秩的关系：
首先，对于矩阵$A$实行行初等变换，不会改变$A$的列向量组的线性相关性和线性组合关系
例题，求向量组的线性相关性，把列向量矩阵华为行标准形，有0行即线性相关
所以，矩阵$A$的秩等于$A$的列向量组的秩
->
向量空间
向量生成的线性空间
基：线性无关，任一向量都可表出
可逆矩阵(可逆变换)不改变向量组的线性相关性$\leftarrow$可逆矩阵等价于一系列初等矩阵的积
向量空间$V$的基实际上是$V$作为向量集合的极大线性无关组
过渡矩阵(基变换矩阵)
坐标变换公式
用初等行变换求$C$（$A^{-1}B$）以及$C^{-1}X$：由过度矩阵可知$B=AC$
$\alpha$关于$A$的坐标为$X$，有$Y=C^{-1}X$：因为坐标变换公式
Euclidean空间 $\mathbb{R}^n$
内积(向量点乘)
Cauchy-Schwarz 不等式
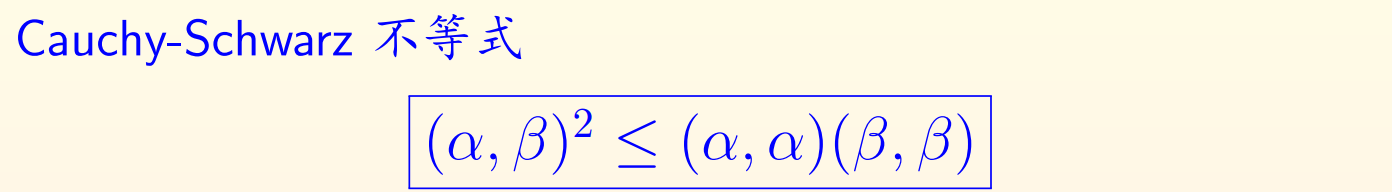
夹角，夹角余弦
正规化
标准正交向量组
把 线性无关向量组 化为 正交向量组的 Gram-Schmidt 正交化方法
Ch4 线性方程组
线性方程组 齐次/非齐次 解
等价的线性方程组
唯一解：
为什么？
Gauss 消元法
线性方程组有解/无解的充要条件：
自由变量
齐次方程组解的结构
解空间$N(A)$
解空间是一个向量空间
解空间的基称为方程组$AX=0$的基础解系
解空间的维数：
基础解系的求法：
在秩不等式中的应用：
非齐次方程组解的结构
非齐次解相减即为齐次解
Ch5 相似矩阵
本章讨论都是方阵
特征向量与特征值
特征值 特征向量 矩阵的特征值等于逆矩阵特征值的倒数,反过来也一样
$$
如果λ是A的一个特征值，对应的特征向量为v，则f(λ)是f(A)的一个特征值，对应的特征向量仍为v。
$$
特征多项式：
特征值：
迹：
特征值和特征向量的求法：
$g(\lambda)$是$g(A)$的特征值：
特征向量的性质
特征向量的线性无关性：简言之，同一个特征值对应的所有特征向量都是线性相关的，不同特征值的特征向量之间一定线性无关
实对称不同特征值对应的特征向量 $\rightarrow$ 彼此正交
重数：
相似矩阵对角化
相似矩阵：
对角化：
可逆矩阵$P$的n个列向量$X_1,X_2,…,X_n$分别是$A$对应于$\lambda_1,…,\lambda_n$的特征向量：
可对角化条件：
应用：一阶齐次线性常系数微分方程组
Ch6 二次型
二次型及其矩阵表示
关于对称矩阵：以主对角线为轴，各元素对应相等
要求二次型为、、、、、、、、、、、、、、、、、矩阵！！！
线性变换：
标准形、规范形
二次型的基本问题：
矩阵合同
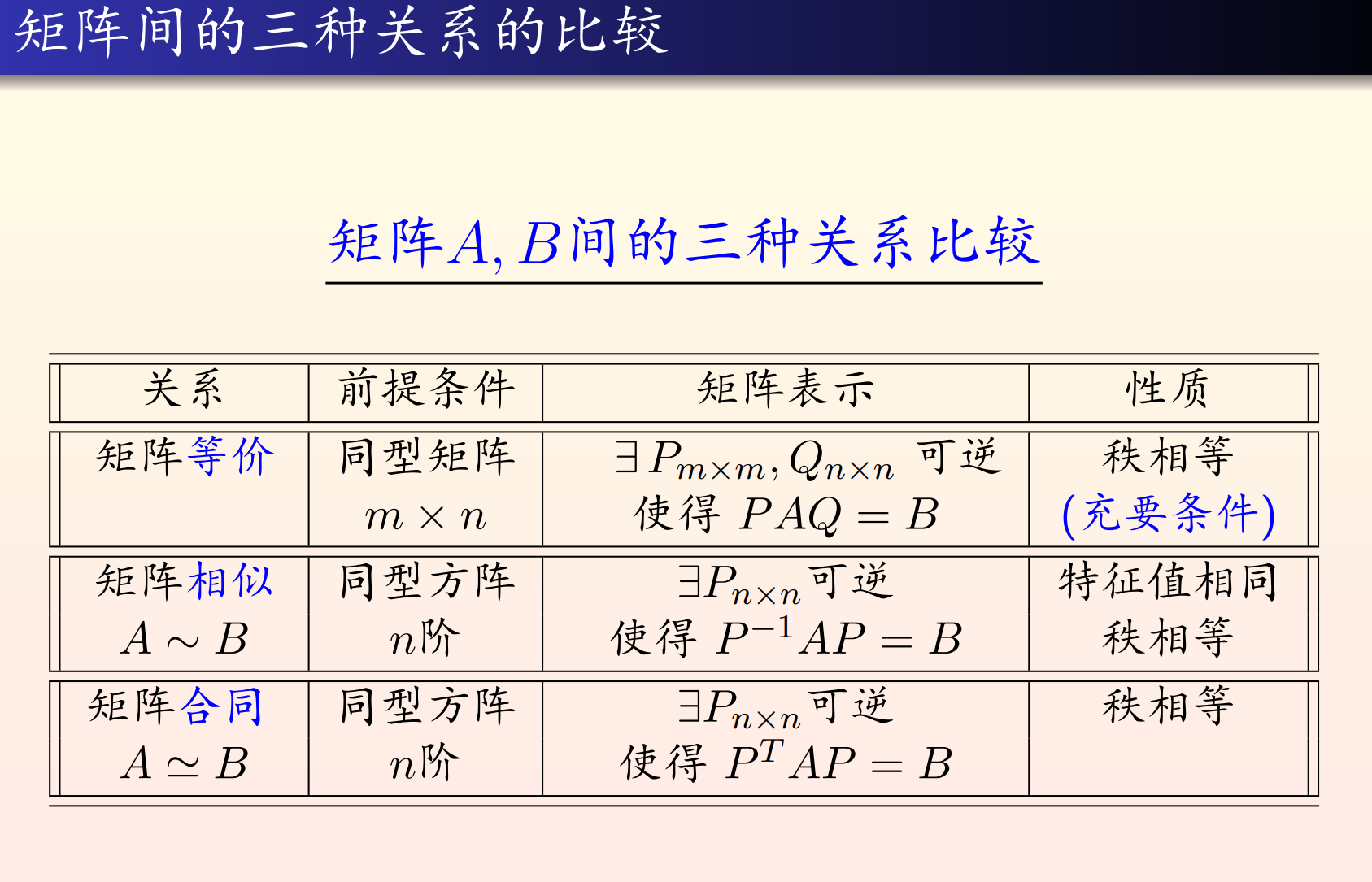
矩阵间的三种关系
正交变换法化二次型为标准形
正交矩阵
正交变换
用正交矩阵得到的矩阵合同同时也是矩阵的相似
主轴定理
用正交变换化二次型为标准形的步骤：
几何意义
二次型的正定性
惯性定理：
惯性指数：
规范形：
对称矩阵合同：
正定二次型：
判断准则：实对称矩阵正定的充要条件是特征值全正
Sylvester定理
正定性判断的几种方式：
正定矩阵主对角元素恒正：
正定矩阵的乘积(也正定)：
