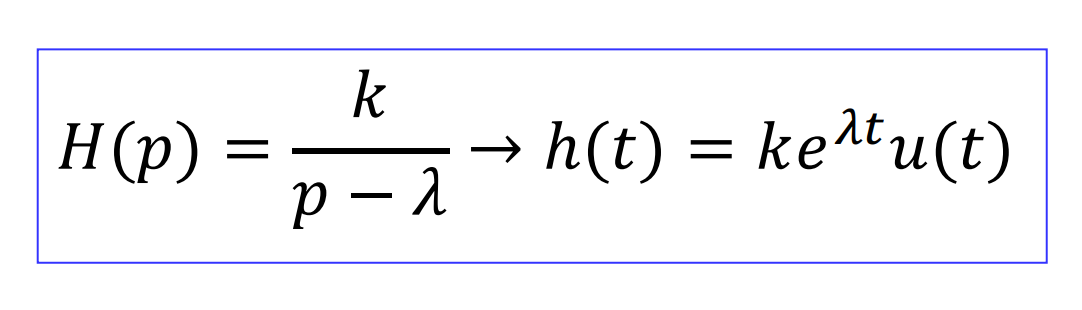Ch.1 绪论
信号
周期信号
信号的平均功率
能量信号与功率信号：
系统
What is a System?
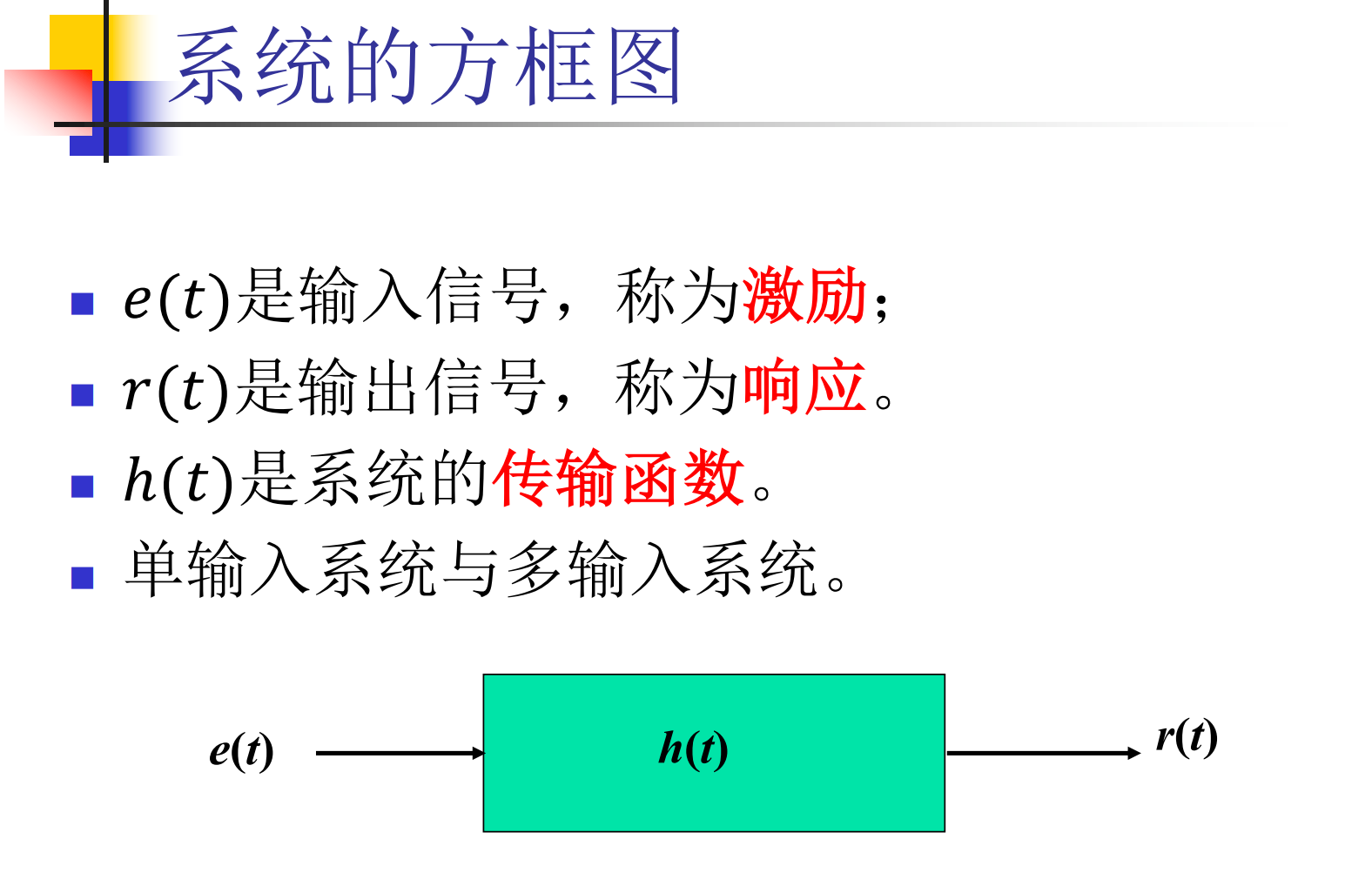
线性系统与非线性系统
线性系统：就是具有齐次性和叠加性的系统
零输入响应和零状态响应
时不变系统：响应形状不随激励的施加时间而改变
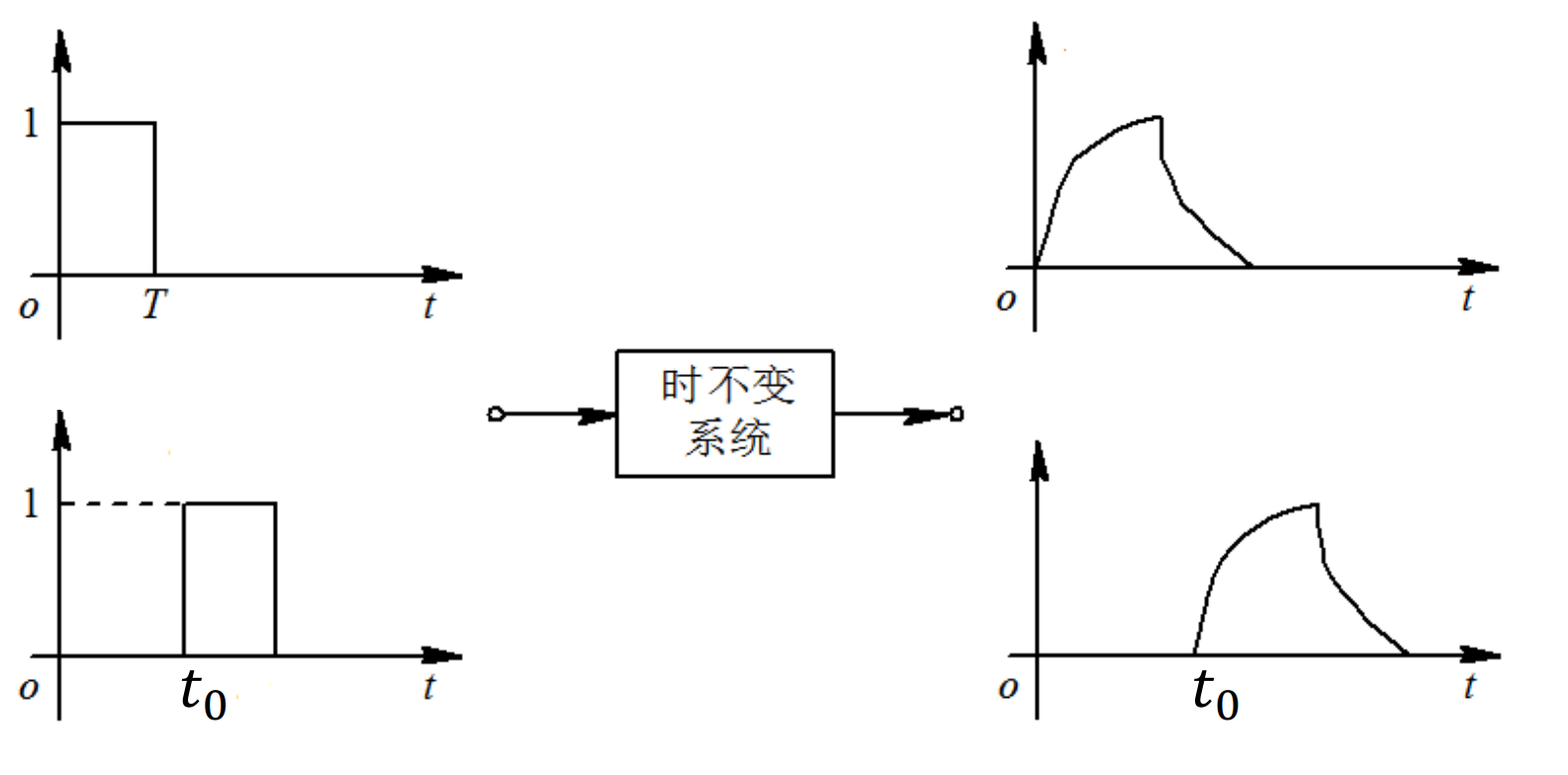
因果系统：响应不早于激励的系统
Ch.2 连续系统的时域分析
线性时不变系统的数学模型 $\rightarrow$ 线性常系数微分方程
经典法：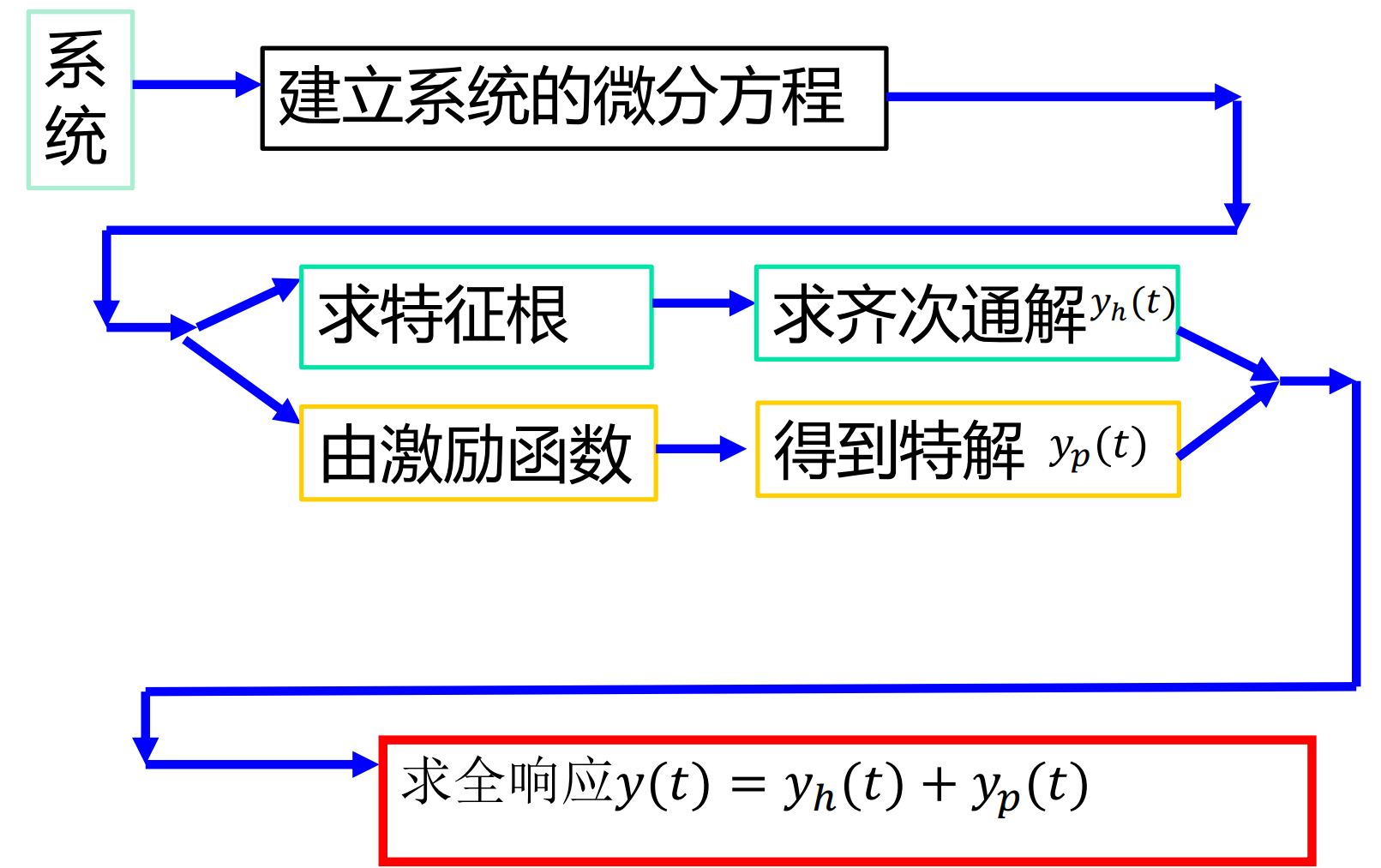
ZIR / ZSR 方法：
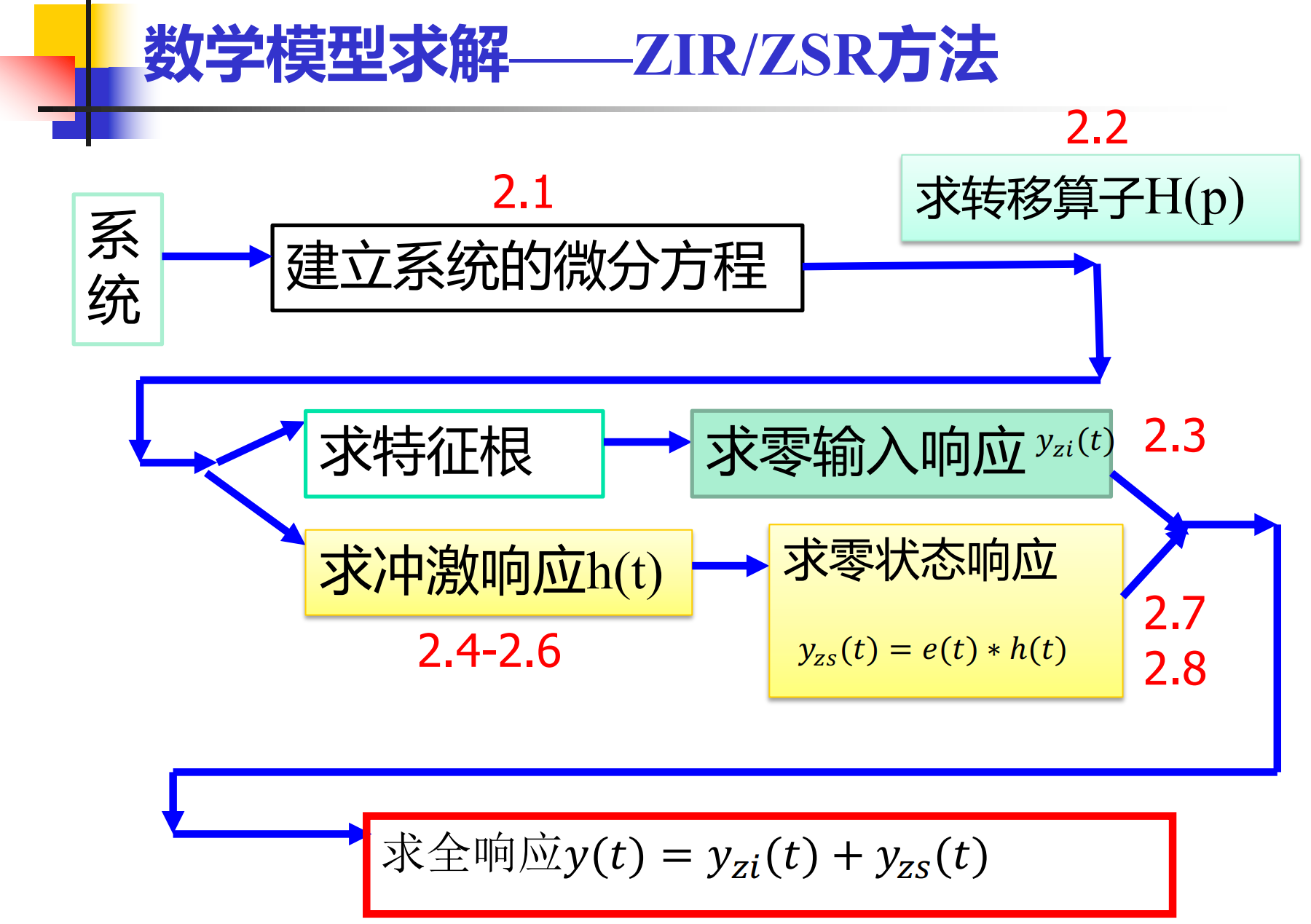
算子表示法 转移算子
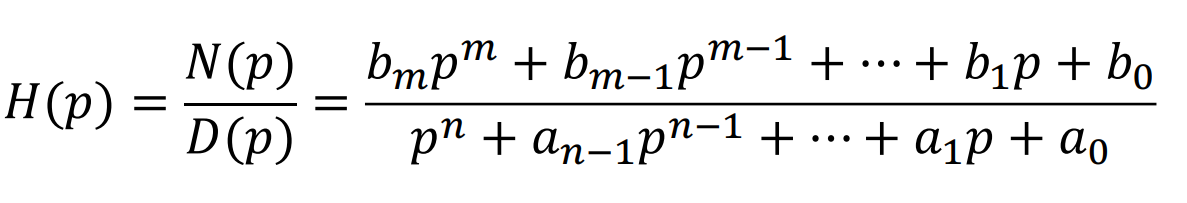
算子的性质
- p多项式可以展开和因式分解
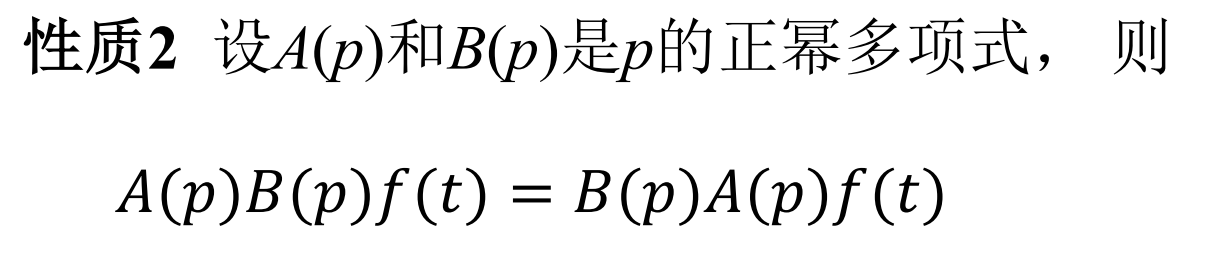
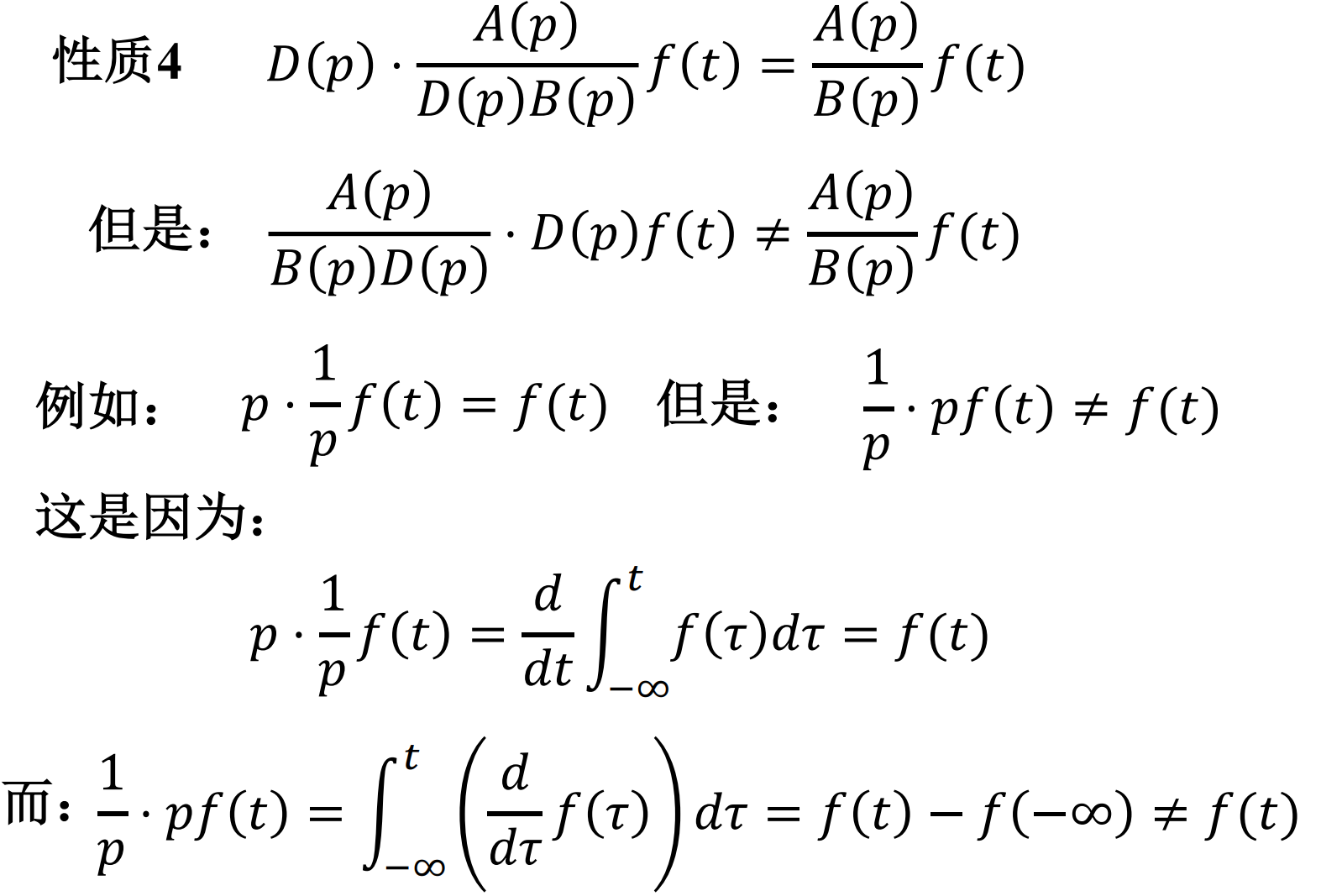
零状态 vs 零输入：
零输入响应求解：与齐次通解求法相同，待定系数直接由初始条件求出
奇异函数：
- 单位斜变 $R(t)$
- 单位阶跃 $ \varepsilon(t) / u(t)$
- 方波(门函数) $G(t)$
- 单位冲激
- 冲击偶信号
单位冲激响应$h(t)$
通过单位冲激响应来判断系统的因果性
单位阶跃响应$r_\epsilon(t)$
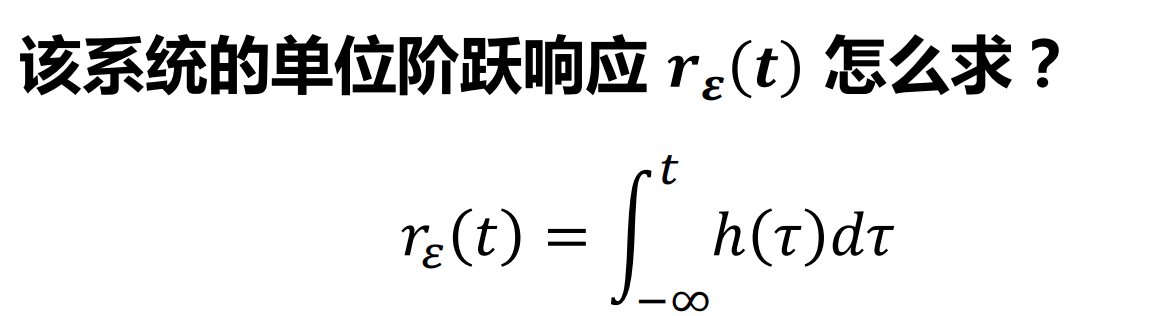
求单位冲激响应
即：求$D(p)h_0(t)=\delta(t)$时，按照$D(p)h_0(t)=0$和附加的初始条件来求零输入即可
例题：
转移算子 部分分式
冲激响应：部分分式分解法，对转移算子$H(p)$分解
简单系统：
一些零状态响应的激励 / 响应对照：
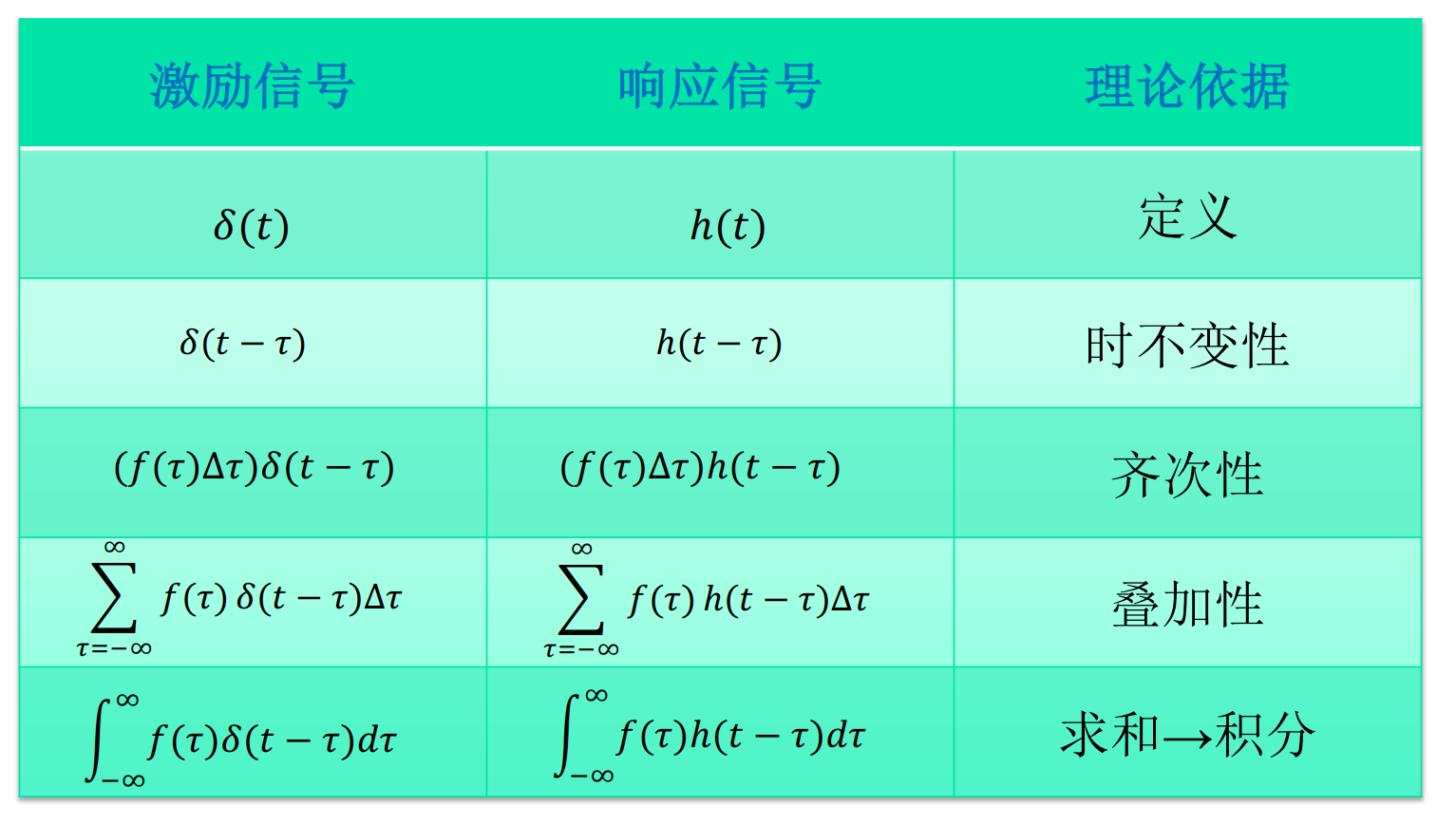
卷积
卷积的图解法：
卷积的性质：
卷积的微分与积分：
常用公式：(当有一函数可化为冲击函数时) $$ f_{1}(t) * f_{2}(t)=\frac{d f_{1}(t)}{d t} * \int_{-\infty}^{t} f_{2}(\tau) d \tau $$ 奇异信号的卷积特性:
零输入响应 零状态响应
自然相应 受迫响应
瞬态响应 稳态响应…
Ch.3 连续信号的正交分解
函数的正交
常见的完备正交函数集
傅里叶级数
傅里叶积分 $ \rightarrow $ 傅里叶变换
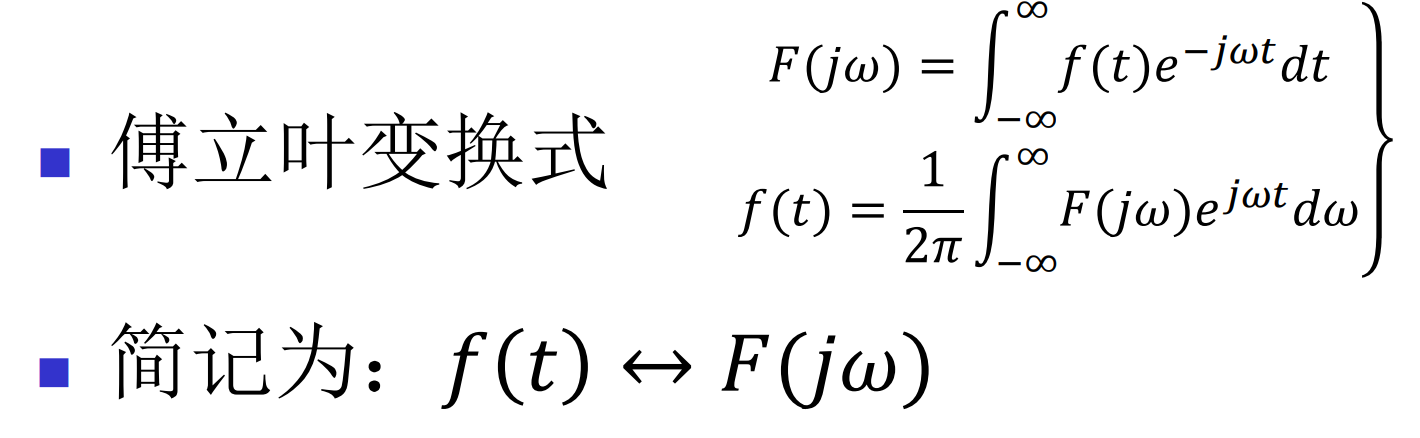
傅里叶变换式：
单边指数函数：
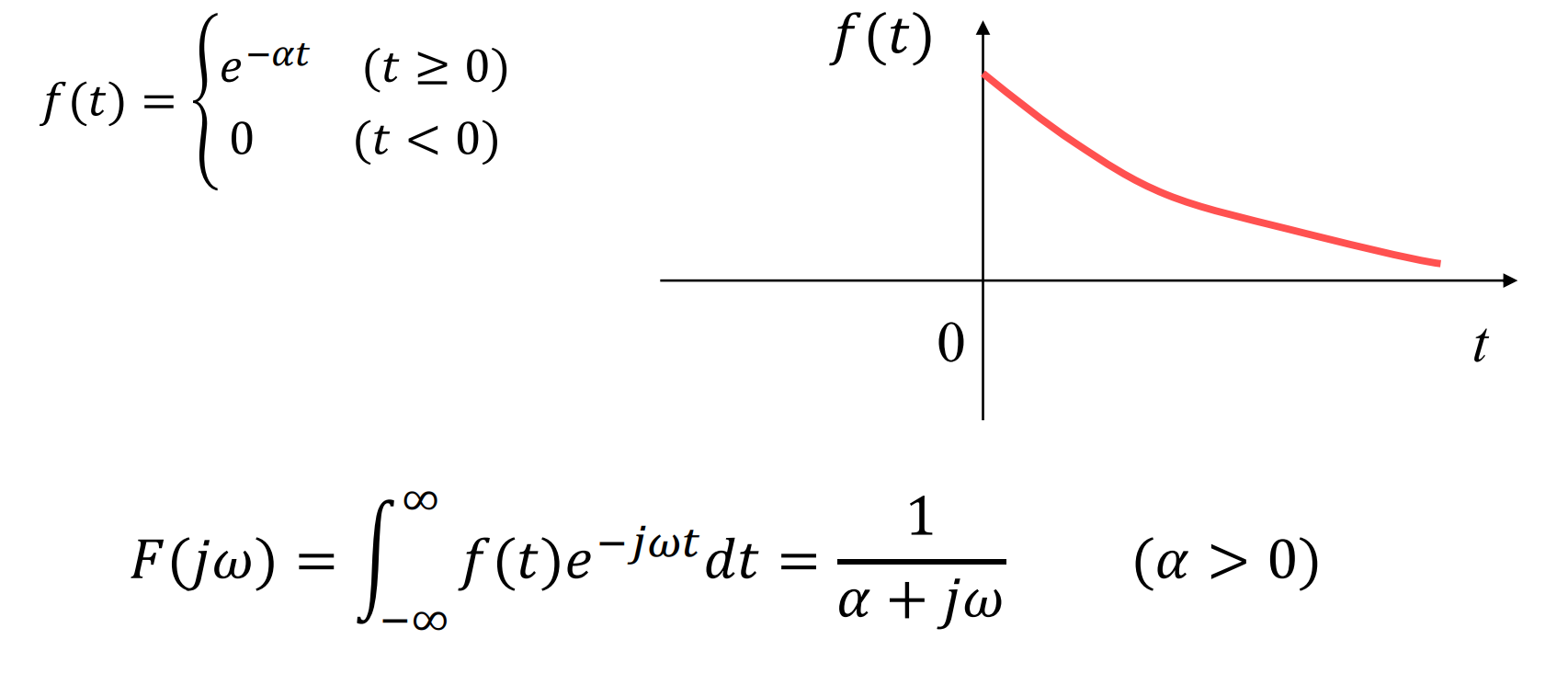
双边指数信号
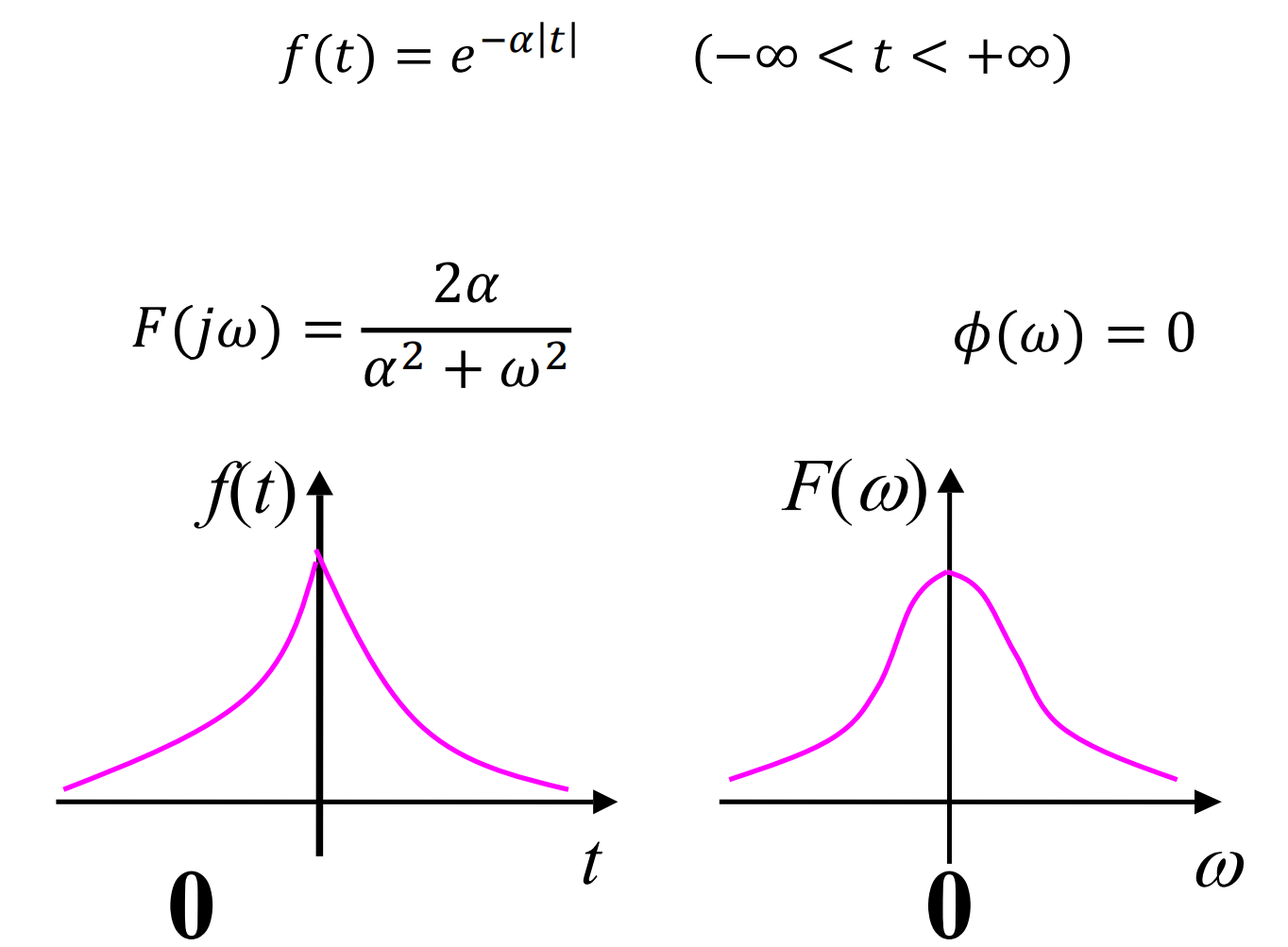
单位冲激： $$ \delta(t) \leftrightarrow 1 $$
傅里叶变换的特性：
- 线性特性：略
- 延时特性
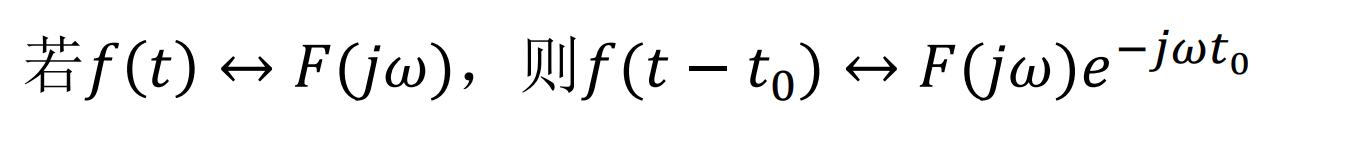
- 移频
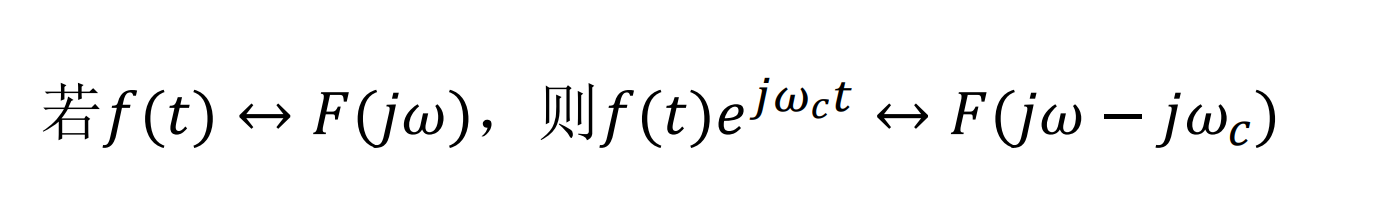
- 尺度变换
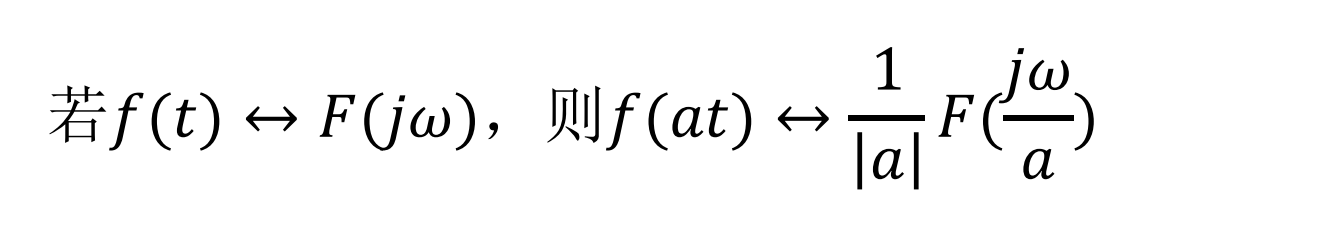
- 奇偶
- 对称
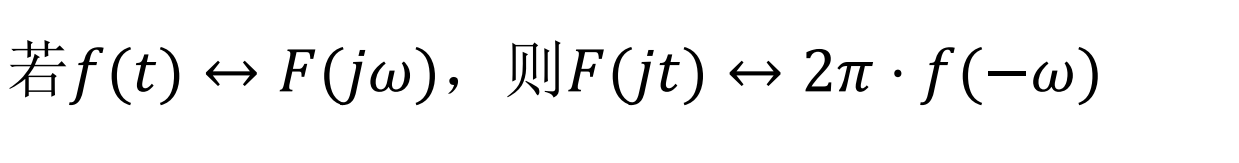
- 微分：
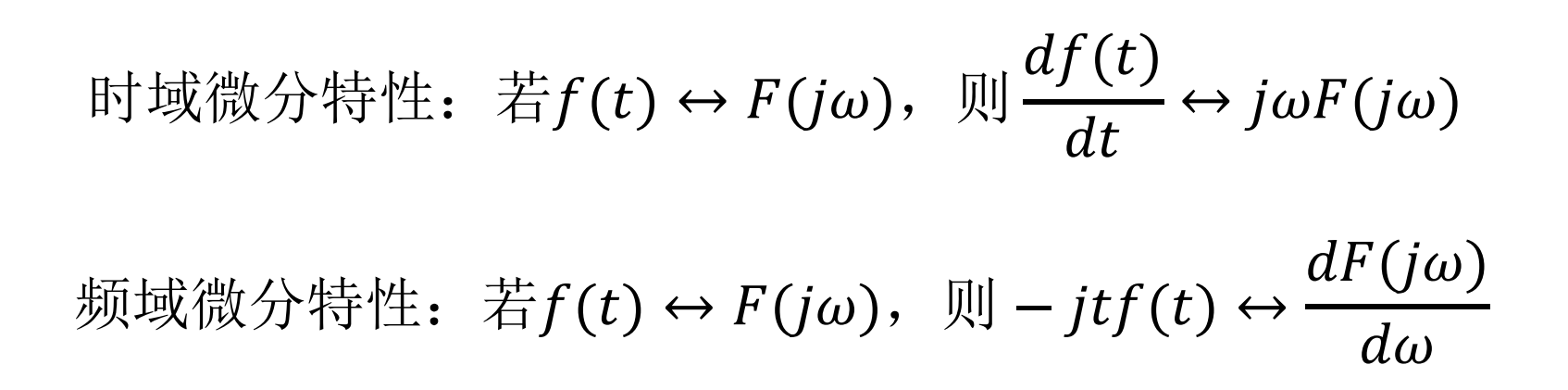
- 积分
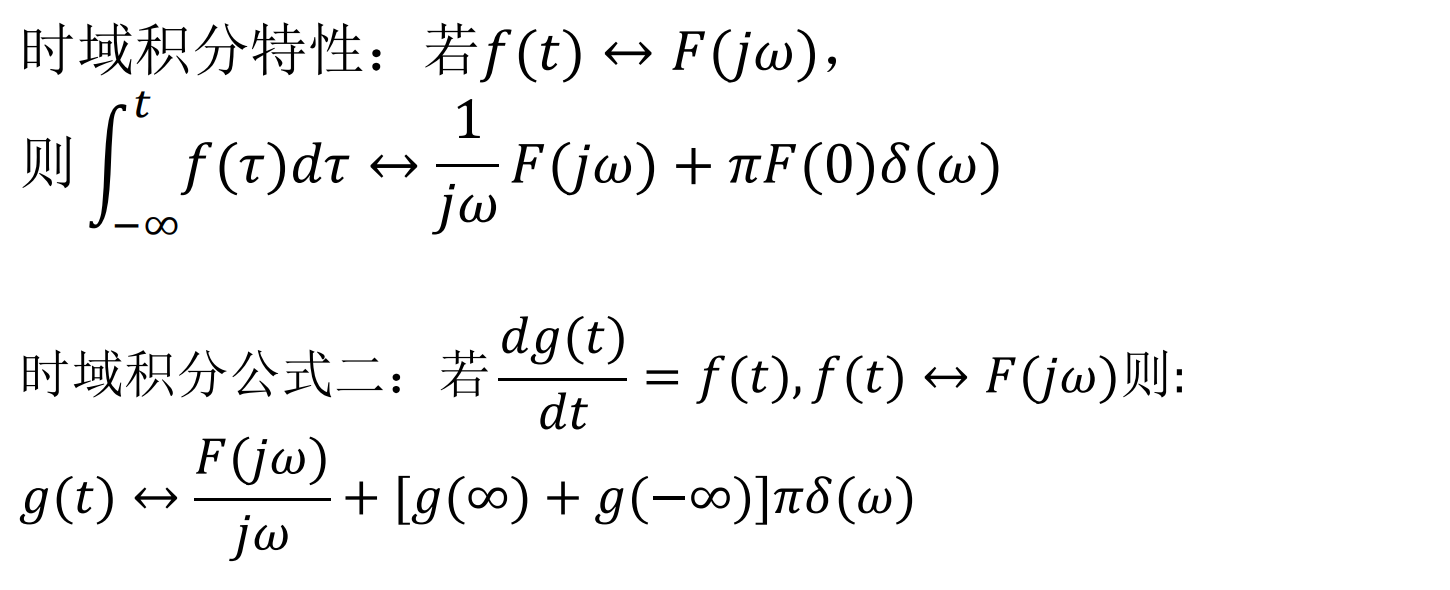
卷积定理：
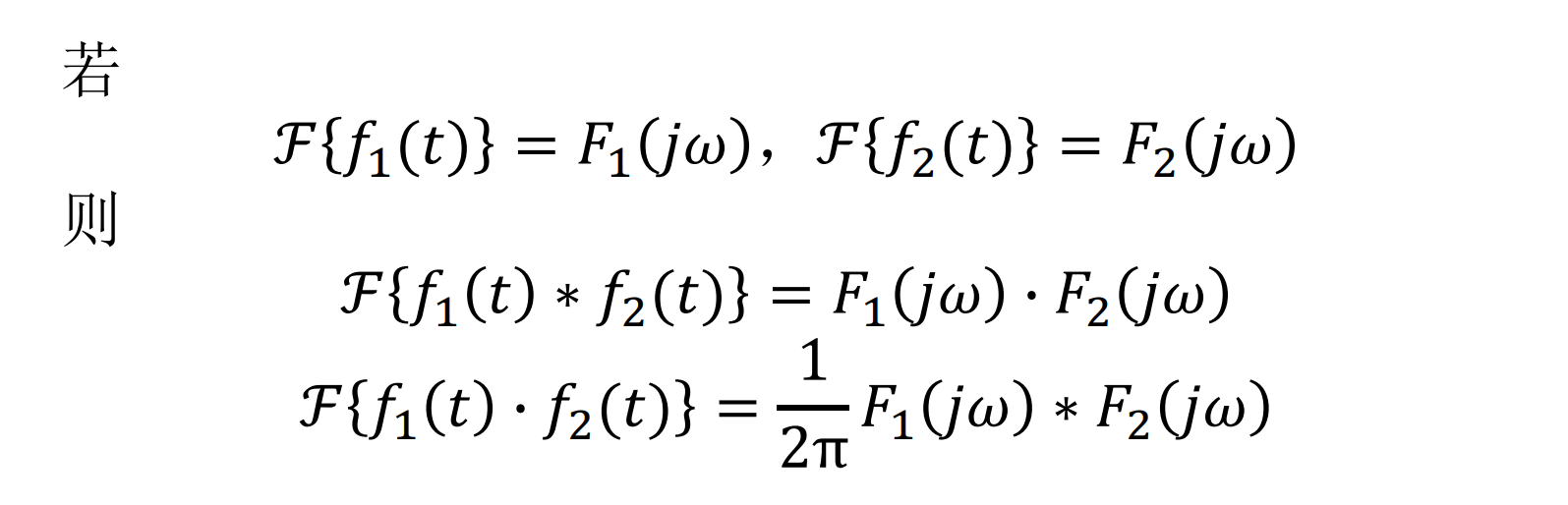
Parseval’s定理
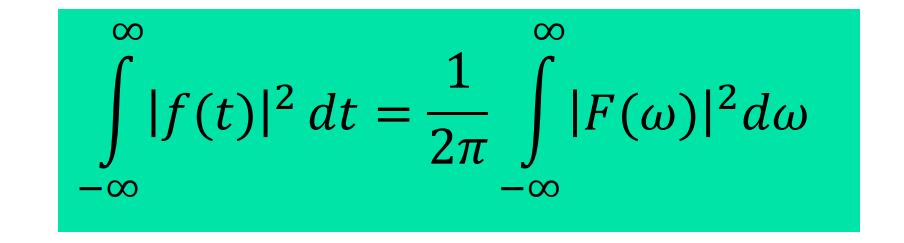
Ch.4 连续时间系统的频域分析
频域分析法与系统函数
$$
\Rightarrow
$$
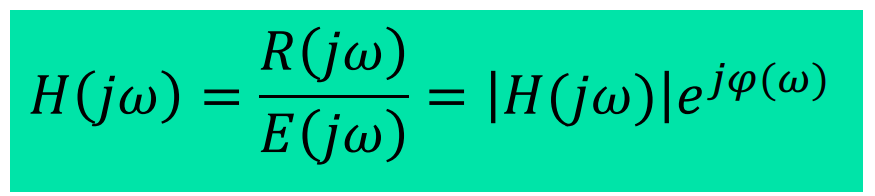
频域分析步骤：
Ch.5 连续时间系统的复频域分析
拉普拉斯变换
与傅里叶变换的关系？
单边拉普拉斯变换：拉普拉斯变换指的是单边变换，变换下限从$0^{-}$开始
常见信号的拉普拉斯变换
- 性质
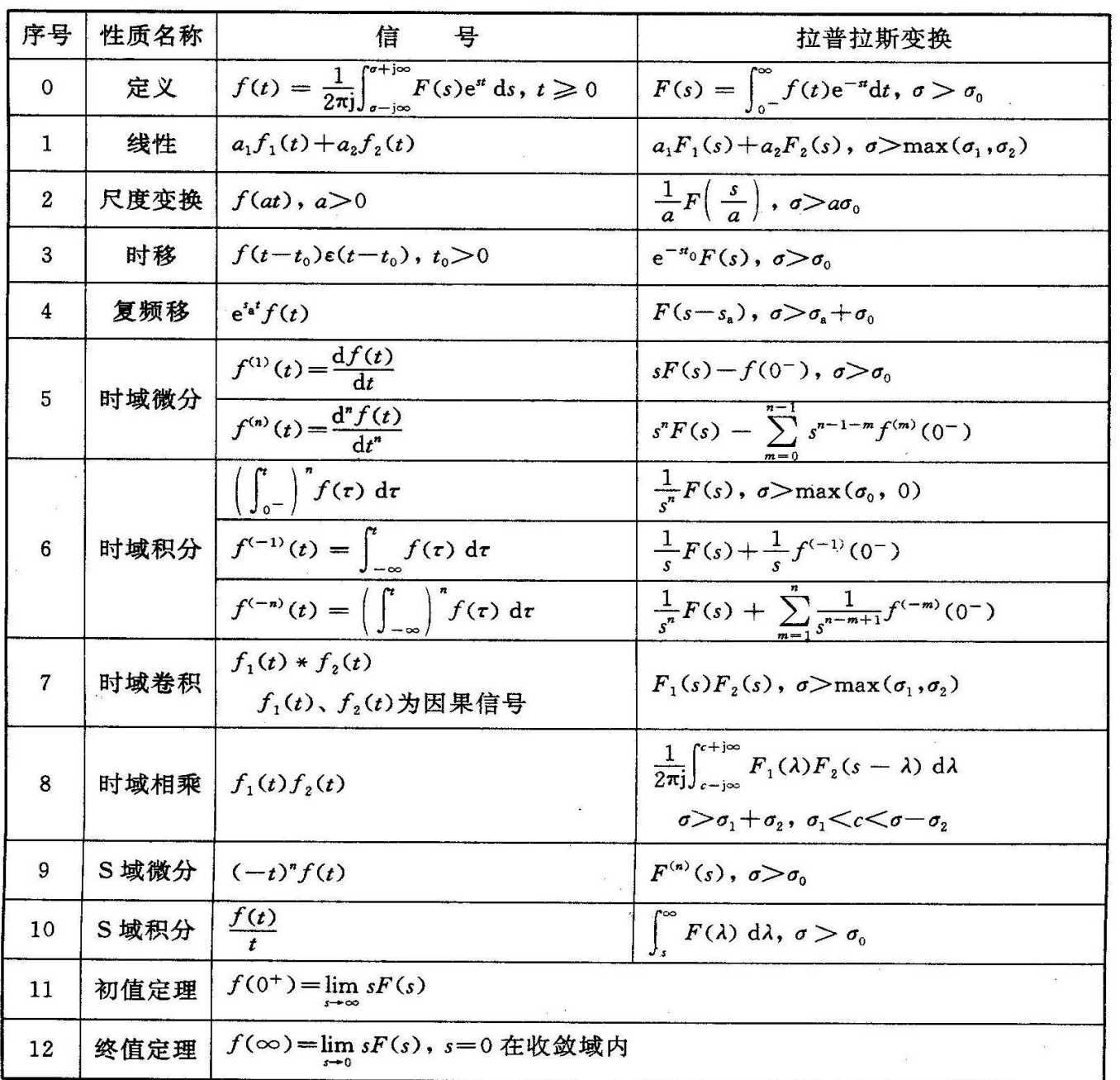
拉普拉斯逆变换
留数法
部分分式展开法
系统函数
初值定理和终值定理的要点：
画图，把n导数和系数的画法背下来
Ch.6 连续时间系统的系统函数
极零点
z-p点分布与频响特性
线性系统的稳定性
对于任何有界的输⼊，其响应也是有界的。
Ch.7 离散时间系统的时域分析
理想抽样
香农取样定理
离散信号
- 单位阶跃序列
- 矩形序列
- 指数序列
- 正弦序列
- 复指数序列
离散信号的变换和运算
移序算子
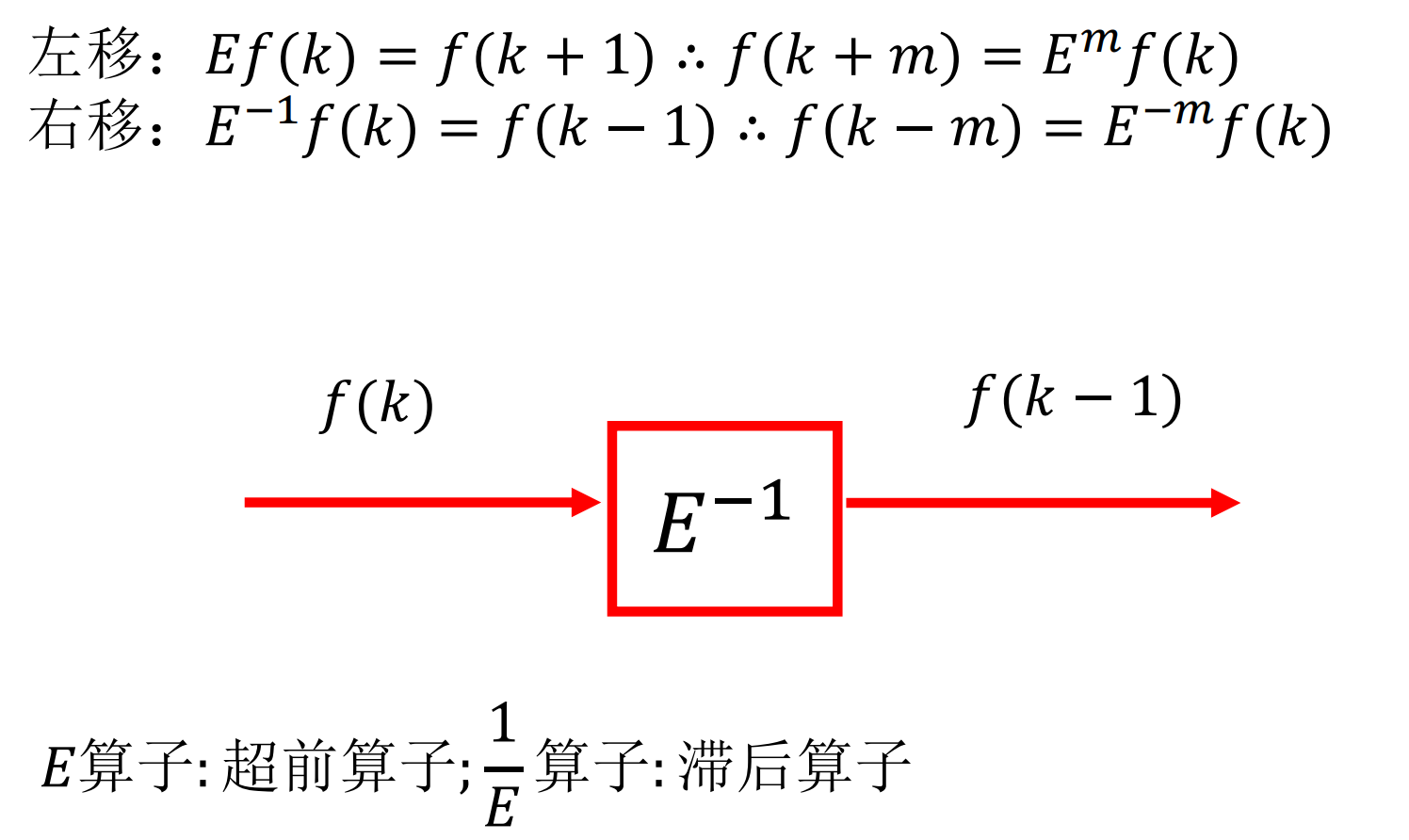
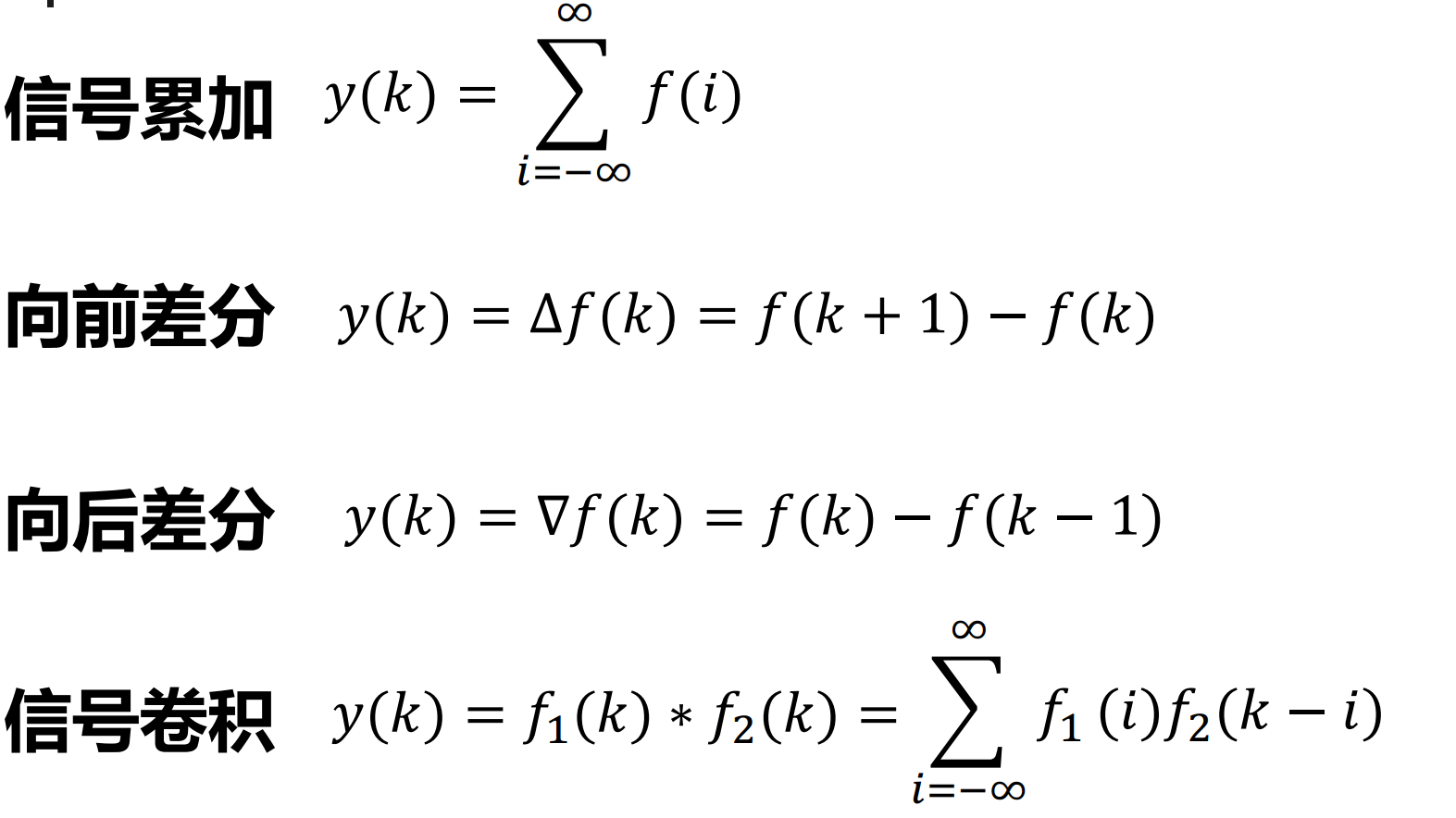
差分算子
典型序列的差分：类似于求导
连续和离散之间的近似：
离散时间系统用差分方程来描述
线性移不变离散时间系统
常系数差分方程求解
迭代法
经典法：特征根，通解+特解
通解：
特解：
ZIR / ZSR 方法：
零输入：由初始条件求得的齐次解
离散时间系统的单位样值响应：
求$h(n)$关键在于，在n=0时将接入的激励转化为起始条件，即x(0), x(-1)..的值
卷积和
性质
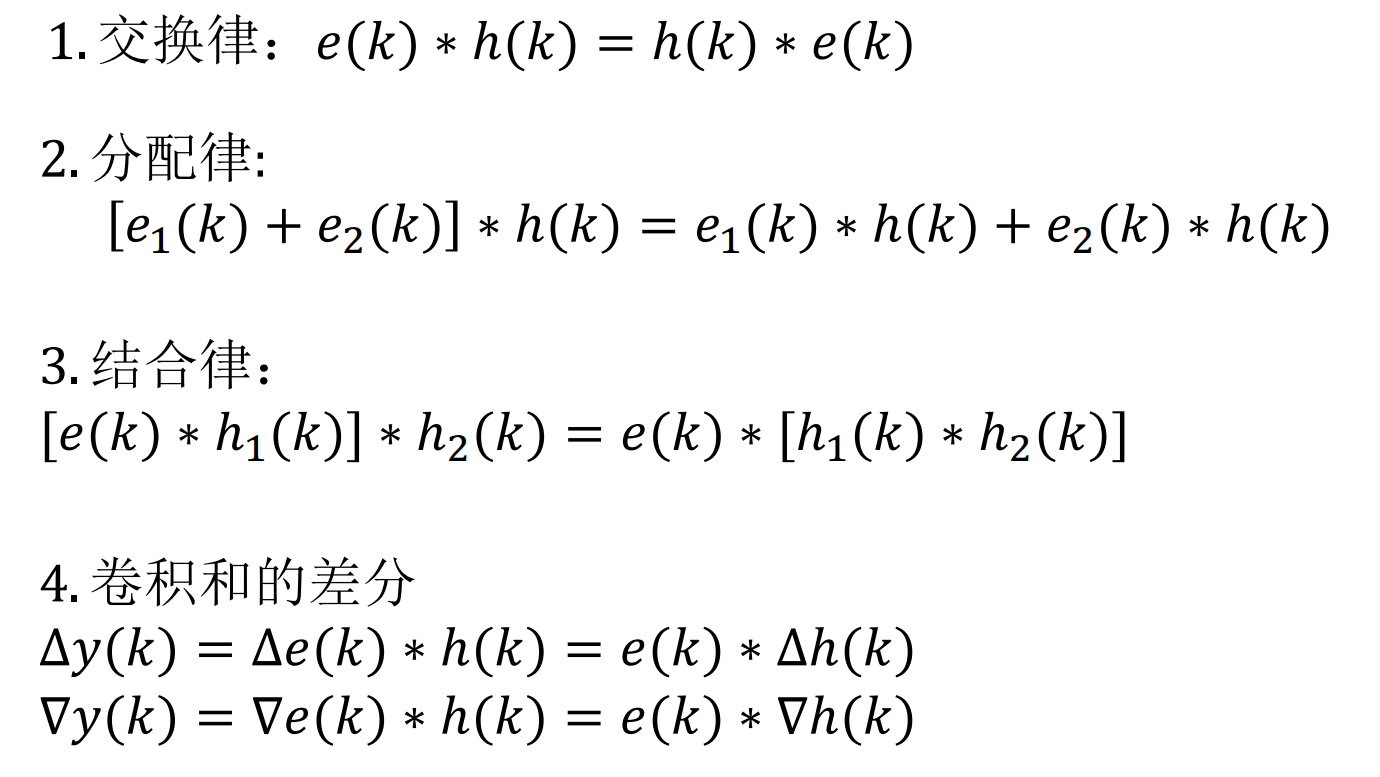
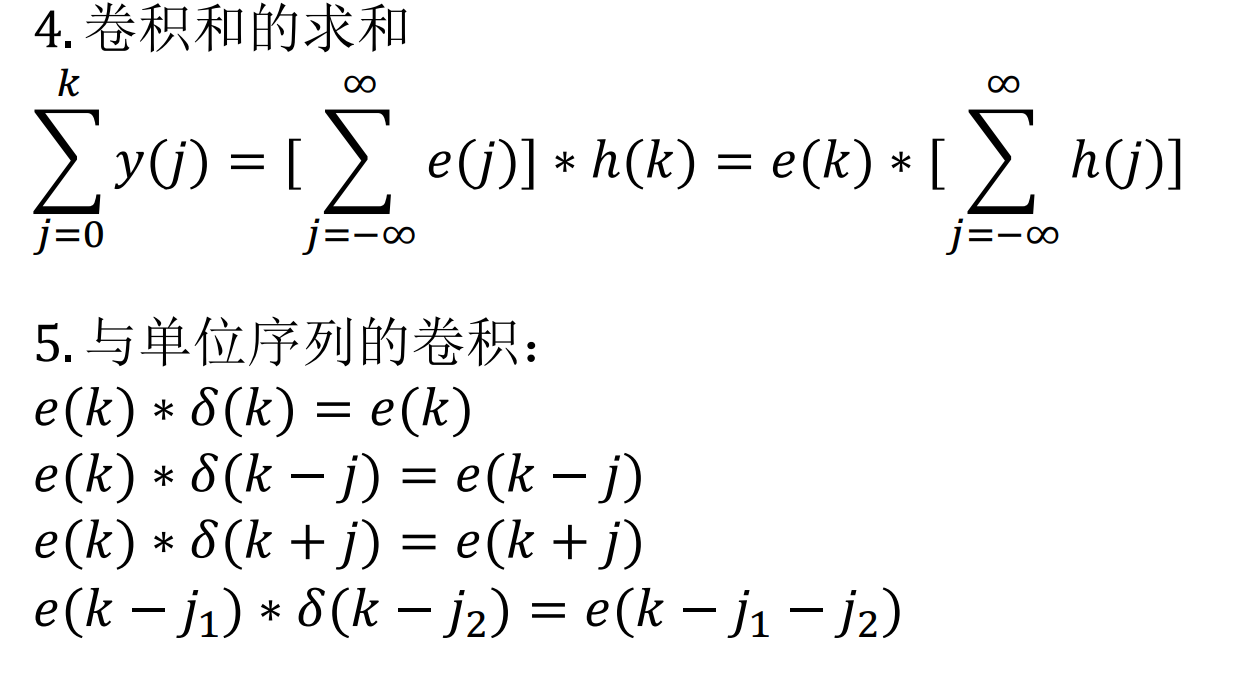
Ch.8 离散时间系统的变换域分析
Z变换
典型序列的Z变换
- 单位样值序列
- 单位阶跃序列、单边指数序列
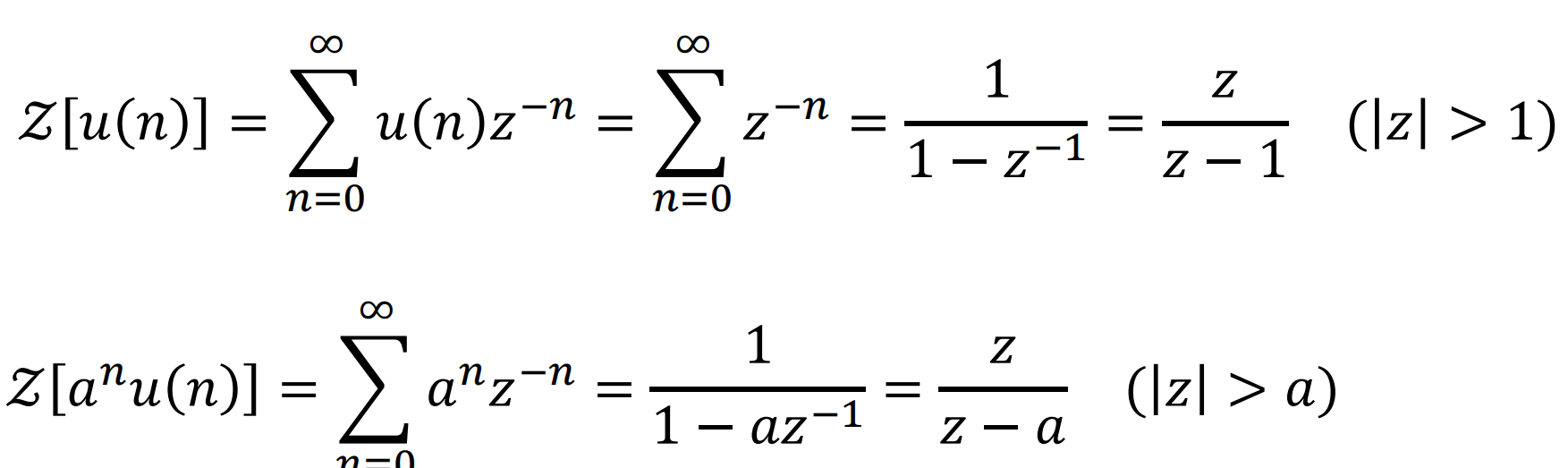
性质：
- 正弦序列Z变换
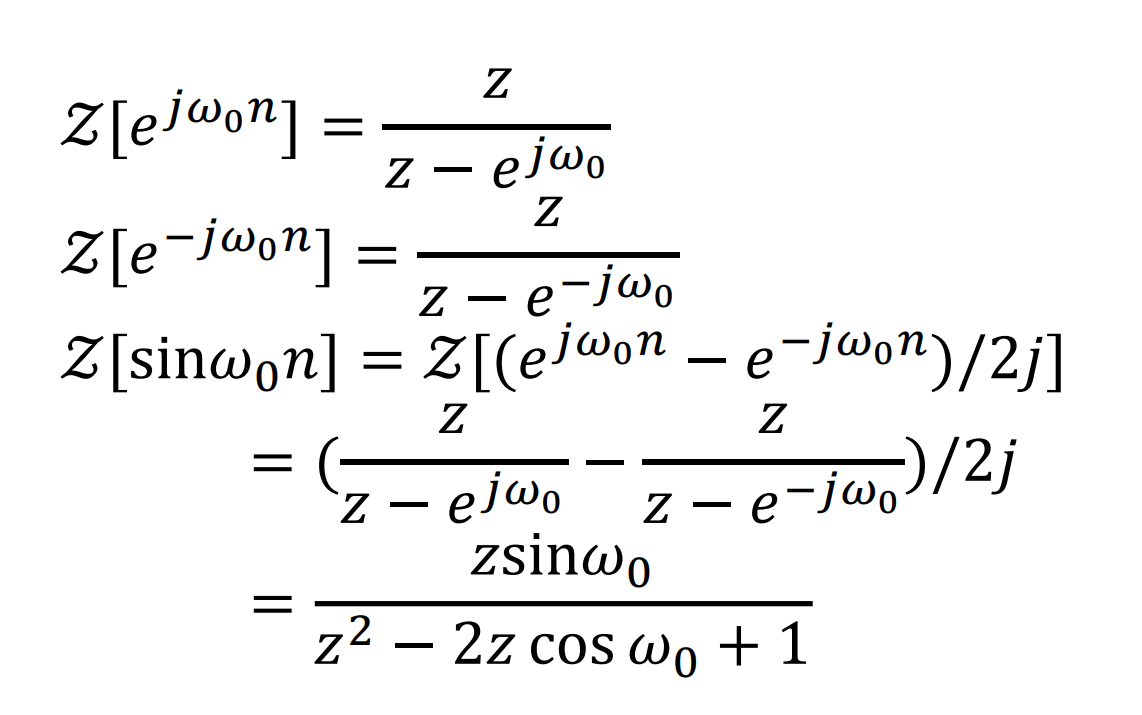
- 时移性质
对离散时间信号, 若有: $$ f(n) \Leftrightarrow F(z) $$ 则 $$ \begin{array}{c} f(n+1) \Leftrightarrow z(F(z)-f(0)) \ f(n+l) \Leftrightarrow z^{l}\left(F(z)-\sum_{i=0}^{l-1} f(i) z^{-i}\right) \end{array} $$
- 尺度变换
- 微分：
- 卷积
- 初值定理和终值定理
逆Z变换
questions
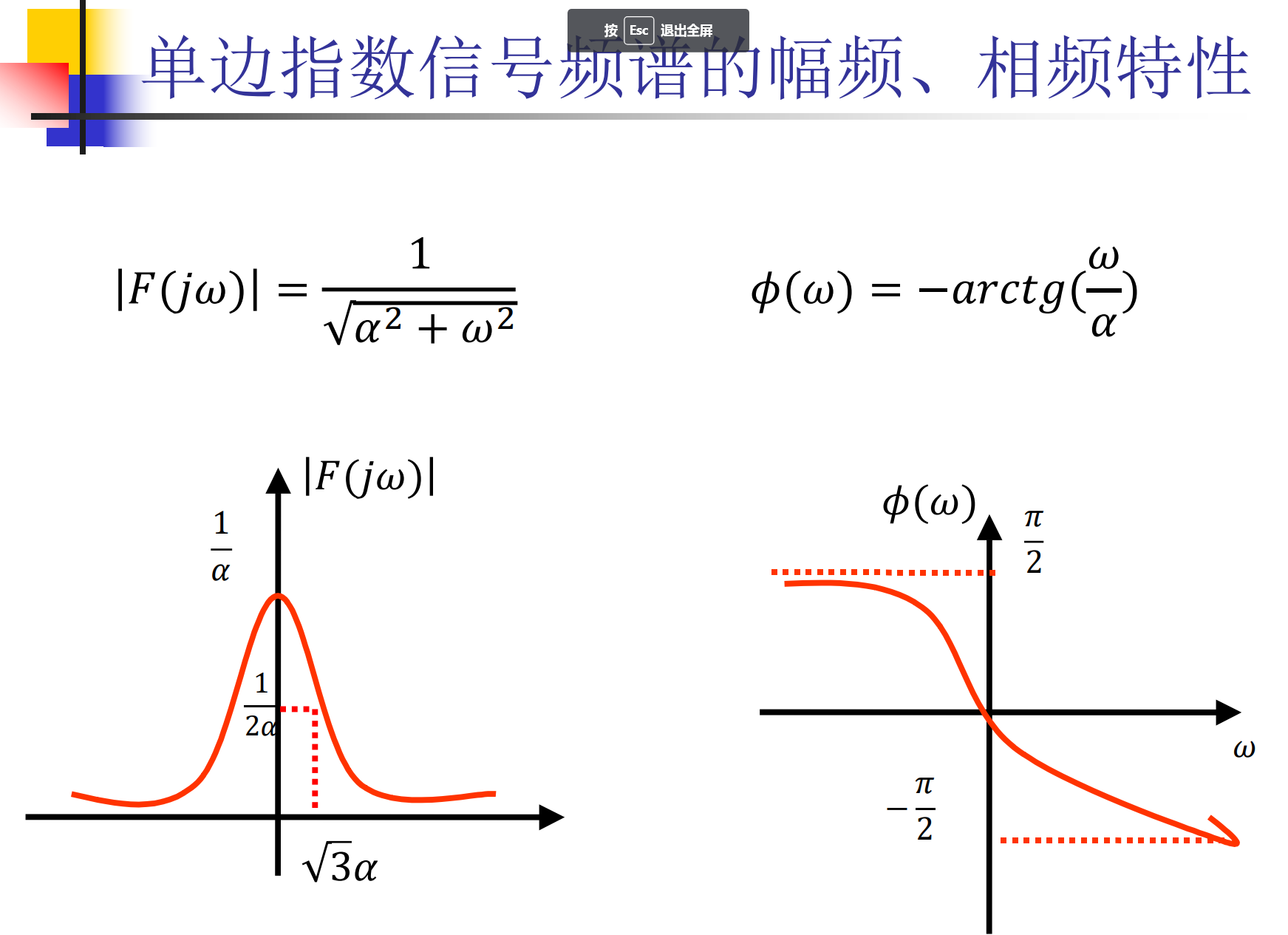
什么是相频？
冲激响应为什么和零输入响应这么像？
